高速フーリエ変換(FFT)をおじさんもC++で作ってみたよ

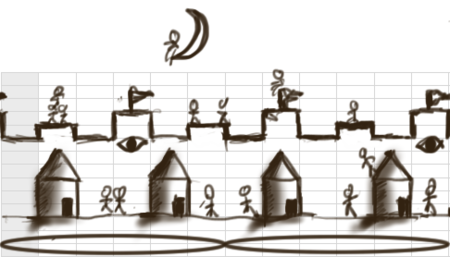
やあ子どもたち。数値配列を日常的に扱っている俺達プログラマーにとって、フーリエ変換がいかに簡単かというイメージを忘れないように以前日記を書きました。その中で、DFT（離散フーリエ変換）計算の実践実装例も見ました。
そして今日はその高速版、FastFourierTransform（高速フーリエ変換）（以下、FFT）の実装及び原理を紹介します。（実際に動くC++のプログラムソースコードは本記事の一番最後の方にあります。）
FFTは20世紀の10大アルゴリズムの中にも数えられる、とても有名なアルゴリズムでもあります。とはいえその歴史は古く、FFTやDFTの本当の起源というところまで行くと、あの大数学者ガウス（1777年生まれ）が既に気付いていた？などという噂もあるらしく、それ自体をテーマにした研究論文が出版されたりしているほどです。ですがひとまず、J.W.Cooley、J.W.Tukeyらが1965年に出した、"An algorithm for the machine calculation of complex Fourier series."(Math. of Comput. vol. 19, pp. 297-301, April, 1965)という論文が現在のFFTのさしあたっての最近の起源とされる向きがあるようです。
FFTはDFTの高速版です。つまり、DFTとの違いはこれが単にその高速化版であること、計算が速いということ、がまず言えます。出力や計算結果の精度に関して何ら違いはありません。（後述でも明らかになるように、速いからと言って近似計算とかではありません。）そしてDFTとの違い、もう一つあって、それはFFTでは入力数値列の長さが２のべき乗数になっていなくてはならないという制約条件があることです。こればっかりはなかなか大きな制約ですが、その条件が満たされている限りは、これら2通りの実装は、同じ入力に対して全く同じ出力結果を返します。
どのくらい高速なのかというと、DFTで、O(N^2)の計算効率のところ、FFTではO(NlogN)となります。（この場合のlogは底数２を想定しています）底が2のlog100は6と7の間なので、これが意味する所は、要素数が100のDFT計算が10倍強速くなり、要素数1万のDFT計算は1000倍（100倍ではなく1000倍です）近く高速化されるということです。つまり、世の中のあらゆる場面において非常に有用なのです。20世紀を代表する10大アルゴリズムの一つに数えられるのもわかろうというものですよね。
なので、高速にDFTの計算をしたい場合は、数値配列の長さを２のべき定数にするなど頑張って工夫して、FFTを使う、ということが一般的に行われます。（世に医療画像診断のMRIやCTの画像などで解像度に512や1024といったサイズが好んで使われるのもこのためではという噂があるほどです）

やさしいFFTアナライザの使い方

作者:公典, 山口,隆彦, 小野
オーム社

Amazon

さてまずは、実装の背景となる、計算原理について説明をします。FFTでは何故かくも高速にDFTと同じ計算が可能なのでしょうか。
それはDanielson-Lanczos Lemmaという式変形を使ってDFTの定義式を書き直すことから始まります。では見て行きましょう。DFTの定義式はこうでした。

・・・(1)
（この最初の数式のレンダリングだけcodecogsを使ってみました。やっぱり綺麗だよね。でもいちいち画像貼っつけるの面倒くさいので後は、はてダのデフォルト数式で行きます。）
そしてこれについて、以下のように変形できるよと言っているのが、Danielson-Lanczos Lemma（以下、DL-Lemma）です。
$\normalsize \begin{equation} F(k)=\sum_{j=0}^{\frac{N}{2}-1}f(2j) e^{-\frac{2\pi k2j}{N}i} + \sum_{j=0}^{\frac{N}{2}-1}f(2j+1) e^{-\frac{2\pi k(2j+1)}{N}i}\end{equation}$ ・・・(2)
DL-Lemmaでは何をしているかというと、線形和として表されるDFTの式を、偶数番目の項と奇数番目の項に分解して書きなおすということをします。(1)式でjを0からNまで数えていたものを、(2)式でのjは0からN/2-1までの数えとして、2jと、2j+1の項に分けて書き直しているだけです。ここで(2)の式変形をもう少し進めます。
$\normalsize F(k)=\sum_{j=0}^{\frac{N}{2}-1}f(2j) e^{-\frac{4\pi kj}{N}i} + \sum_{j=0}^{\frac{N}{2}-1}f(2j+1) e^{-\frac{4\pi kj+2\pi k}{N}i}$
$\normalsize =\sum_{j=0}^{\frac{N}{2}-1}f(2j) e^{-\frac{4\pi kj}{N}i} + e^{-\frac{2\pi k}{N}i}\sum_{j=0}^{\frac{N}{2}-1}f(2j+1) e^{-\frac{4\pi kj}{N}i}$ ・・・(2a)
$\normalsize = F_e(k) + W_N^kF_o(k)$ ・・・(2b)
(2a)式または(2b)式まで書いて、DL-Lemmaとして紹介されることが多いようです。この(2b)式の表現では、言うまでもありませんが、それぞれ、
$\normalsize F_e(k) = \sum_{j=0}^{\frac{N}{2}-1}f(2j)e^{-\frac{4\pi kj}{N}i}$ ,・・・(3)
$\normalsize F_o(k) = \sum_{j=0}^{\frac{N}{2}-1}f(2j+1)e^{-\frac{4\pi kj}{N}i}$ ,・・・(4)
$\normalsize W_N^k = e^{-\frac{2\pi k}{N}i}$ ・・・(5)
という具合に、記号を導入して簡略化しています。Fの下付き文字の"e"と"o"は、それぞれ、”even”（偶数）、”odd”（奇数）の頭文字をとったものです。
ここで、(2b)式つまり(2a)式をさらに分解することを考えます。そのために、同じようにして、(3)式、(4)式を、それぞれ、DL-Lemmaを使って分解します。分解して書いているだけで、内容はもとの分解前の式そのものです。まずは(3)式のF_e(k)を、さらに偶数番目の項と奇数番目の項とに分解することを考えてみよう。
$\normalsize F_e(k) = \sum_{j=0}^{\frac{N}{4}-1}f(2(2j))e^{-\frac{4\pi k(2j)}{N}i}+\sum_{j=0}^{\frac{N}{4}-1}f(2(2j+1))e^{-\frac{4\pi k(2j+1)}{N}i}$
$\normalsize = \sum_{j=0}^{\frac{N}{4}-1}f(4j)e^{-\frac{8\pi kj}{N}i}+e^{-\frac{4\pi k}{N}i}\sum_{j=0}^{\frac{N}{4}-1}f(4j+2)e^{-\frac{8\pi kj}{N}i}$ ・・・(3a)
$\normalsize = F_{ee}(k) + W_{\frac{N}{2}}^kF_{eo}(k)$ ・・・(3b)
でここでも言うまでもないが、(3a)→(3b)の中で、
$\normalsize F_{ee}(k)=\sum_{j=0}^{\frac{N}{4}-1}f(4j)e^{-\frac{8\pi kj}{N}i}$ ,・・・(6)
$\normalsize F_{eo}(k)=\sum_{j=0}^{\frac{N}{4}-1}f(4j+2)e^{-\frac{8\pi kj}{N}i}$ ,・・・(7)
という具合に、記号を導入しています。
次に同じようにして、(4)式のF_o(k)を、DL-Lemmaを使って、偶数番目の項と奇数番目の項とに分解して書きなおします。
$\normalsize F_o(k) = \sum_{j=0}^{\frac{N}{4}-1}f(2(2j)+1)e^{-\frac{4\pi k(2j)}{N}i}+\sum_{j=0}^{\frac{N}{4}-1}f(2(2j+1)+1)e^{-\frac{4\pi k(2j+1)}{N}i}$
$\normalsize =\sum_{j=0}^{\frac{N}{4}-1}f(4j+1)e^{-\frac{8\pi kj}{N}i}+e^{-\frac{4\pi k}{N}i}\sum_{j=0}^{\frac{N}{4}-1}f(4j+3)e^{-\frac{8\pi kj}{N}i}$ ・・・(4a)
$\normalsize = F_{oe}(k) + W_{\frac{N}{2}}^kF_{oo}(k)$ ・・・(4b)
でここでも言うまでもないが、(4a)→(4b)の中で、
$\normalsize F_{oe}(k)=\sum_{j=0}^{\frac{N}{4}-1}f(4j+1)e^{-\frac{8\pi kj}{N}i}$ ,・・・(8)
$\normalsize F_{oo}(k)=\sum_{j=0}^{\frac{N}{4}-1}f(4j+3)e^{-\frac{8\pi kj}{N}i}$ ,・・・(9)
という具合に、記号を導入しています。
はい。いかがだろうか。(2b)式に(3a)(4a)(5)式を適用して全部大真面目に展開しちゃうと、めちゃめちゃ長くてみづらいため、(2b)式に(3b)(4b)式を代入してみると、
$\normalsize F(k) = F_{ee}(k) + W_{\frac{N}{2}}^kF_{eo}(k) + W_N^kF_{oe}(k) + W_N^kW_{\frac{N}{2}}^kF_{oo}(k)$ ・・(10b)
さて、(2b)式を、(1)式のDL-Lemmaレベル１展開と呼ぶならば、(10b)式は(1)式のレベル２展開とでも呼ぶべきものであるね。では、レベル３展開はどんな式になるだろう？(2b)式とこの(10b)式を見てるだけで推測できやしないか。そのために(10b)を偶数項と奇数項に分けて書き直してみよう。(10b)の第2項と第3項の順番を入れ替えて、以下のように書きなおしてみることにする。
$\normalsize F(k) = F_{ee}(k) + W_N^kF_{oe}(k) + W_{\frac{N}{2}}^kF_{eo}(k) + W_{\frac{N}{2}}^kW_N^kF_{oo}(k)$ ・・(10c)
これを見て気付くべき推測ロジックとしてはこうだ。まずレベル1の(2b)式中の各Fを見て、その下付き添字列にさらにeをつけ足したもので置き換える。これでレベル2の偶数項は完成だ。次にレベル2の奇数項は、レベル1の(2b)式の各Fについて、eではなくoをその下付き添字列に追加し、さらに、新しいW値を掛算する。（。。というルールは(2b)式そのものであることに気付こう。）
つまり、以上は、(2b)式の各項に、(2b)式自身を適用した結果が、(10c)式となることが確認できましたというだけの話。
同じ方針を使うことでレベル２展開の(10c)式から推測でき、実際そうなるレベル３展開の式はこうだ。
$\normalsize F(k) =\\ F_{eee}(k) + W_N^kF_{oee}(k) + W_{\frac{N}{2}}^kF_{eoe}(k) + W_{\frac{N}{2}}^kW_N^kF_{ooe}(k) + W_{\frac{N}{4}}^kF_{eeo}(k) +\\ W_{\frac{N}{4}}^kW_N^kF_{oeo}(k) + W_{\frac{N}{4}}^kW_{\frac{N}{2}}^kF_{eoo}(k) + W_{\frac{N}{4}}^kW_{\frac{N}{2}}^kW_N^kF_{ooo}(k)$ ・・(11c)
レベル４展開まで書いてある説明はなかなかないが、mimetexの文字列をコピペするだけなのでここではレベル４も書いてみる。
$\normalsize F(k) =\\ F_{eeee}(k) + W_N^kF_{oeee}(k) + W_{\frac{N}{2}}^kF_{eoee}(k) + W_{\frac{N}{2}}^kW_N^kF_{ooee}(k) +\\ W_{\frac{N}{4}}^kF_{eeoe}(k) + W_{\frac{N}{4}}^kW_N^kF_{oeoe}(k) + W_{\frac{N}{4}}^kW_{\frac{N}{2}}^kF_{eooe}(k) +\\ W_{\frac{N}{4}}^kW_{\frac{N}{2}}^kW_N^kF_{oooe}(k) +W_{\frac{N}{8}}^kF_{eeeo}(k) + W_{\frac{N}{8}}^kW_N^kF_{oeeo}(k) +\\ W_{\frac{N}{8}}^kW_{\frac{N}{2}}^kF_{eoeo}(k) + W_{\frac{N}{8}}^kW_{\frac{N}{2}}^kW_N^kF_{ooeo}(k) + W_{\frac{N}{8}}^kW_{\frac{N}{4}}^kF_{eeoo}(k) +\\ W_{\frac{N}{8}}^kW_{\frac{N}{4}}^kW_N^kF_{oeoo}(k) + W_{\frac{N}{8}}^kW_{\frac{N}{4}}^kW_{\frac{N}{2}}^kF_{eooo}(k) +\\ W_{\frac{N}{8}}^kW_{\frac{N}{4}}^kW_{\frac{N}{2}}^kW_N^kF_{oooo}(k)$
・・・(12c)
これを見てどうというよりも、ルールさえおさえてしまえば再帰的にどこまでも数式展開ができてしまうことが実感できるだろうか。
さて次は、F_eeや、F_eee、F_eeeeをどうするかついて考えてみよう。
レベル１に関しては(3)式(4)式、レベル２に関しては(6)〜(9)式にあえて書いてみたが、これを見て気づかなくてはならないことがある。それは、(3)式(4)式におけるNが２の時、あるいは(6)〜(9)式におけるNが４の時、Σの上の数はゼロとなり、つまり
$\normalsize F_{xxx(x='e'or'o')..}=\sum_{j=0}^{0}{ "Function of (j<--0)"}$
こんな状況になり、Σの中身についてはj=0とするだけでよいことになる。なので、Nが２の各べき乗値をとるとき、（はい、ここで、「とるとき」と書きましたが、以降ではもうそれが前提です。「とるとき」の話しか書いてありません。つまりこの前提がそのまま、冒頭文に記述した、FFTの制約条件になってくるわけです！）F(k)を展開した式は、ぶっちゃけ以下のように書ける。そう、それぞれこんな簡単な式にぶっちゃけてしまえるのである。
（N=2のとき、(2a)式と(2b)式より）
$\normalsize F(k)=f(0)+W_2^kf(1)$ ・・・(13)
（N=4のとき、(6)〜(9)式と(10c)式より）
$\normalsize F(k)=f(0)+W_4^kf(1)+W_2^kf(2)+W_2^kW_4^kf(3)$ ・・・(14)
さて、N=8以降は、ここまで、F_eee、F_eeeeを具体的な式として求めてはいないので、(13)式(14)式からルールを見出すことにしよう。すると、f()の中の添字は、DL-Lemmaにて、jという添字が2jと2j+1という添字に展開されることを考えれば、つまり「既存の添字値列を２倍した並びと、既存の添字値列を２倍して１を足したものの並びに新しいW値を掛け算したものを、並べて書けば、次のレベルの展開式になる」というルールが見いだせるはずだ。

●「二進数のビット反転」について
上の「f()の中の添字」列の決め方は、0,1,2,3..（２のべき定数）　という整数列の各要素を2進数で表したときに、以下の手順をするのと同等なことがわかる。
①各整数値の2進数表記の1桁目で静的ソートし、真ん中で区切って２グループとする。
②さらに①の各グループの中で、各整数値の2進数表記の2桁目で静的ソートし、真ん中で区切って２グループとする。
③さらに②の各グループの中で、各整数値の2進数表記の3桁目で静的ソートし、真ん中で区切って２グループとする。
（以上、を２進数の桁数分だけ、果てしなく繰り返す。）
以上の最終的な結果（図の一番下の0,4,2,6,1,5,3,7）は本来の数え数列（0,1,2,3,4,5,6,7)の２進数表記時の桁並びを逆さにし、小さい値順にまた並べなおしたものになるという話。つまりビット反転で計算することもできるなと。図にするとこんな感じ。

ちなみにこの添字列は上の本文の方法で計算してもよいし、あるいはビット反転から求めてもいいのだけど、これってNがわかった時点で一度だけ計算しておけばいい数値列なので、どう計算しようがどのみちあまりパフォーマンスには効いてこない話なんだよね。（本記事末尾の実装例の前処理計算部分では、前者の方法を採用しているよ）

なので、
（N=8のとき）（(11c)式より）
$\normalsize F(k)=f(0)+W_4^kf(2)+W_2^kf(4)+W_2^kW_4^kf(6)+W_8^kf(1)+\\W_4^kW_8^kf(3)+W_2^kW_8^kf(5)+W_2^kW_4^kW_8^kf(7)$ ・・・(15)
となる。ここまでくればもうプログラムに起こせてしまう気もしてくるのだが、あえてN=16のときも書けば、
（N=16のとき）（(12c)式より）
$\normalsize F(k)=f(0)+W_4^kf(4)+W_2^kf(8)+W_2^kW_4^kf(12)+W_8^kf(2)+\\W_4^kW_8^kf(6)+W_2^kW_8^kf(10)+W_2^kW_4^kW_8^kf(14)+W_{16}^kf(1)+\\W_4^kW_{16}^kf(5)+W_2^kW_{16}^kf(9)+W_2^kW_4^kW_{16}^kf(13)+W_8^kW_{16}^kf(3)+\\W_4^kW_8^kW_{16}^kf(7)+W_2^kW_8^kW_{16}^kf(11)+W_2^kW_4^kW_8^kW_{16}^kf(15)$
・・・(16)
となる。
さて今まで頑張って展開してきたF(k)のkというものは、0〜N-1の値をとる（k=0→(N-1)) ものなので、FFTの計算はつまり、F(0)〜F(N-1)の値を全て計算してやることで完了する。
なのでこれまた実際に各Nの場合について書きだしてみよう。
（N=2の場合）(13)式より
$\normalsize F(0)=f(0)+W_2^0f(1)\\F(1)=f(0)+W_2^1f(1)$ ・・・2式まとめて→(17)とする
（N=4の場合）(14)式より
$\normalsize F(0)=f(0)+W_4^0f(2)+W_2^0f(1)+W_2^0W_4^0f(3)\\F(1)=f(0)+W_4^1f(2)+W_2^1f(1)+W_2^1W_4^1f(3)\\F(2)=f(0)+W_4^2f(2)+W_2^2f(1)+W_2^2W_4^2f(3)\\F(3)=f(0)+W_4^3f(2)+W_2^3f(1)+W_2^3W_4^3f(3)$
・・・４式まとめて→(18)とする
（N=8の場合）(15)式より
$\normalsize F(0)=f(0)+W_8^0f(4)+W_4^0f(2)+W_4^0W_8^0f(6)+W_2^0f(1)+\\W_2^0W_8^0f(5)+W_2^0W_4^0f(3)+W_2^0W_4^0W_8^0f(7)\\F(1)=f(0)+W_8^1f(4)+W_4^1f(2)+W_4^1W_8^1f(6)+W_2^1f(1)+\\W_2^1W_8^1f(5)+W_2^1W_4^1f(3)+W_2^1W_4^1W_8^1f(7)\\F(2)=f(0)+W_8^2f(4)+W_4^2f(2)+W_4^2W_8^2f(6)+W_2^2f(1)+\\W_2^2W_8^2f(5)+W_2^2W_4^2f(3)+W_2^2W_4^2W_8^2f(7)\\F(3)=f(0)+W_8^3f(4)+W_4^3f(2)+W_4^3W_8^3f(6)+W_2^3f(1)+\\W_2^3W_8^3f(5)+W_2^3W_4^3f(3)+W_2^3W_4^3W_8^3f(7)\\F(4)=f(0)+W_8^4f(4)+W_4^4f(2)+W_4^4W_8^4f(6)+W_2^4f(1)+\\W_2^4W_8^4f(5)+W_2^4W_4^4f(3)+W_2^4W_4^4W_8^4f(7)\\F(5)=f(0)+W_8^5f(4)+W_4^5f(2)+W_4^5W_8^5f(6)+W_2^5f(1)+\\W_2^5W_8^5f(5)+W_2^5W_4^5f(3)+W_2^5W_4^5W_8^5f(7)\\F(6)=f(0)+W_8^6f(4)+W_4^6f(2)+W_4^6W_8^6f(6)+W_2^6f(1)+\\W_2^6W_8^6f(5)+W_2^6W_4^6f(3)+W_2^6W_4^6W_8^6f(7)\\F(7)=f(0)+W_8^7f(4)+W_4^7f(2)+W_4^7W_8^7f(6)+W_2^7f(1)+\\W_2^7W_8^7f(5)+W_2^7W_4^7f(3)+W_2^7W_4^7W_8^7f(7)$
・・・８式まとめて→(19)とする。
いかがだろうか。以上が実際にコンピュータにさせたい計算の内容だ。以上、ルールも見出したし、あとはプログラムにするだけというところにほとんどもうきてるのだが、計算量を最小限にするという実装的な意味でまだ人類が共有すべきノウハウが２つ３つ残っている。それはWの項の計算についてだ。このW項はTwiddle-Factorと呼ばれるそうで、つまりは複素数平面において原点から生えてる大きさ１のベクトルがくるくると廻ったものの集合となっている。このWの計算コストを最小限にしたいというその１点にのみ、残された実装ノウハウの全ては捧げられている。というか計算量の軽減、高速化こそがFFTの取り柄なので、今までは単なる式変形、ここからがFFTのFFTたる本領の工夫なのだ。ではみて行こう。

(17)(18)(19)式を見て、さらに気づかなくてはならないことがあと３つある。１つ目は、
$\normalsize W_2^1=-W_2^0$
$\normalsize W_4^2=-W_4^0,W_4^3=-W_4^1$
$\normalsize W_8^4=-W_8^0,W_8^5=-W_4^1,W_8^6=-W_4^2,W_8^7=-W_4^3$
・・・まとめて→(20)式とする。
という関係だ。これは、(5)式の定義と複素数の性質から明らかなことだね。これで計算しなきゃいけないW値の数が半減することがわかった。
気づかなくてはならないことの２つ目は、これも(5)式のWの定義式から明らかなことで、
$\normalsize W_8^2=W_8^1W_8^1\\W_8^3=W_8^1W_8^1W_8^1$
$\normalsize W_{16}^2=W_{16}^1W_{16}^1\\W_{16}^3=W_{16}^1W_{16}^1W_{16}^1\\W_{16}^4=W_{16}^1W_{16}^1W_{16}^1W_{16}^1\\W_{16}^5=W_{16}^1W_{16}^1W_{16}^1W_{16}^1W_{16}^1\\W_{16}^6=W_{16}^1W_{16}^1W_{16}^1W_{16}^1W_{16}^1W_{16}^1\\W_{16}^7=W_{16}^1W_{16}^1W_{16}^1W_{16}^1W_{16}^1W_{16}^1W_{16}^1$
・・・まとめて→(21)式とする。
という性質だ。これによって、W値として計算しておかなくてはならないのは、各レベルのk=1のときのW値だけ求めておけばあとはそれを互いに掛け合わせることで、使い回しができるということだ。W値の計算はとても重い処理だが、全部でlogN（対数の底は２）個数のW値だけ計算しておけばよさそうだ。
(17)(18)(19)式を見てさらに気づかなくてはならないことの３つ目はずばり、「同じW値が複数の項にわたって何度も現れるので、計算は階層的に行ったほうが効率がよさそう」・・・式ではないが(22)とする。
だ。そしてこの点がバタフライダイアグラム（butterfly-diagram）と呼ばれるものを人々に描かせた理由だ。バタフライというのは、多分、このダイアグラムを書いてみたら蝶々のように見えてきたからだろうね。
(17)(18)(19)式を見て(20)(21)(22)式を考慮しながらすらすらとプログラム化出来る人はもうそれでいい、そういう人にバタフライダイアグラムは必要ない。バタフライダイヤグラムはそうでない普通の人にも、計算の順番やポイントを整理して見やすくするために書かれた図面であり、いわばアルゴリズムの設計図だ。
DFTは定義式から明らかなように、線形変換なので、(17)(18)(19)式は、どれもそれぞれ、
[F] = [Mat][f]
といった行列式として書けるのだが、そうすると[Mat]の各要素の式がものすごく長くなるので現実的ではない。そこで、[f]がどう階層的に料理されて[F]になるのかを、よりコンパクトに記述したものがバタフライダイヤグラムだ。バタフライダイアグラムでは、[f]を一番左側に、そして[F]を一番右側に書き、処理全体は左から始まり、右に流れていく。そして、一番右側に到達した時点で、計算が終了していることになる。
例によって、各Nの場合のバタフライダイアグラムを考えながらみて行こう。
（N=2のとき）（17式を書きなおしただけ。怖くない）

いかがだろうか。まず、横向きの矢印は、そこまでに流入してきた要素の線形和を表現する。そして横線を跨いでいる斜め線は、そのつけ根の時点での値を他の線形和へコピーして流入させることを意味している。また、横線や斜め線の傍らに書かれた値は、そこを通過する際に、その値を掛け算することを意味している。
ここにさらに、(20)(21)を考慮すればこうなる。

いずれもこれは、この図で何かがわかるということではなくて、ひとえにこれは(17)式から図を起こしたに過ぎない。
同じようにして、他のN値の場合についてもみて行こう。
（N=4のとき）（18式を書きなおしただけ。怖くない）

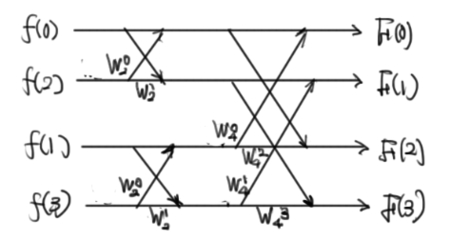
ここにさらに、(20)(21)を考慮すればこうなる。

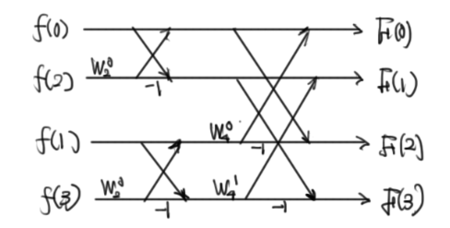
（N=8のとき）（19式を書きなおしただけ。怖くない）

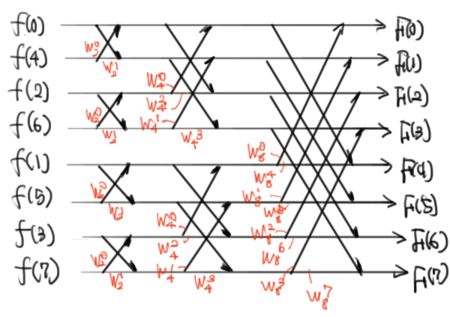
ここにさらに、(20)(21)を考慮すればこうなる。

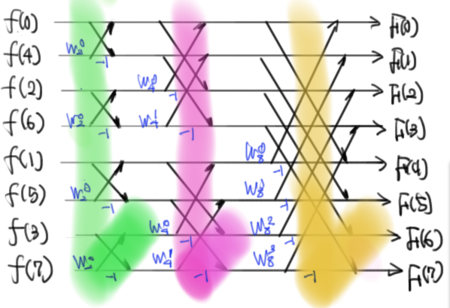
いかがだろうか。N=8の最後の図では、計算の順番、プログラムのループの作り方のヒントとして、縦帯を塗っておいた。Wの値を使いまわすために、このように縦方向に一気に計算してしまって、それが全て終わったら、右にずれる、という流れで組むのが都合いいです。（上の図でいくと、緑→紫→黄色の順に計算を行うイメージ）
最後にフーリエ逆変換について。逆変換の場合は、まず(5)式の指数部のマイナスがなくなります。あとは上述の計算手順を通して全て一緒ですが、最後にFの各要素を、Nで割り算します。（後述の、lc_inverse_fft()の実装部も参照ください。）
さて以上がFFTの計算原理の説明の一切です。続きまして実際に動く実装例と、使用例とを見て行きましょう。

ディジタルフーリエ解析 1 基礎編 (1) [音響入門シリーズ]

作者:城戸健一
コロナ社

Amazon

// "fft.cpp"

#include "fft.h"
using namespace std;

int lc_fft_calc_ids(
                    const int N,
                    vector< int >* pids
                    )
{
    // fft 計算前に一度だけ本関数を使いID並び列情報、ids, n_levelを計算しておきます。
    // ここで得られた ids, n_level を、fftの計算で使用します。
    // 配列サイズが変わらない限りids, n_levelは使い回し可能。
    //【入力】N:入力信号配列の大きさ（２のべき乗）
    //【出力】pids:ID並び（呼出時は空を前提）
    //      戻り値: n_level
    int n_level;
    {
        auto& i = n_level;
        for( i=0; i<64; ++i )// マジック★ナンバー！
            if( N>>i == 1) break;
    }
    vector< int >& ids = *pids;
    // ID 並び列の計算
    ids.reserve( N );
    {
        ids.push_back( 0 );
        ids.push_back( 1 );
        for( int i=0; i<n_level-1; ++i )
        {
            auto sz = ids.size();
            for_each( ids.begin(), ids.end(), [](int& x){ x*=2; } );
            ids.insert( ids.end(), ids.begin(), ids.end() );
            auto it = ids.begin();
            std::advance( it, sz );
            for_each( it, ids.end(), [](int&x){ x+=1; } );
        }// i
    }
    return n_level;
}
void lc_fft(
            const vector< complex<double> >& a,
            const vector< int >& ids,
            const int n_level,
            vector< complex< double > >* pout,
            bool is_inverse/*=0*/
            )
{
    // fft
    // 入力信号 a 数値列の、高速フーリエ変換を行います。
    //【入力】a: 数値列としての離散入力信号、
    //         (a.size()は２のべき乗数であることが大前提)
    //     ids/n_level: 内部使用する情報(lc_fft_calc_iid()の出力)
    //【出力】pout: 数値列としての計算結果。（呼び出し時は空を前提）
    //【オプション】is_inverse：直接は使わないで下さい。
    //      逆変換には、lc_fft_inverse()を使用します。
    auto N = a.size();
    auto& F = *pout;
    {
        F.resize( N );
        for( int i=0; i<N; ++i )
            F[ i ] = a[ids[i]];
    }
    unsigned int po2 = 1;
    for( int i_level=1; i_level<=n_level; ++i_level )
    {
        po2<<=1;
        const int po2m = po2>>1;
        // 高価なexp()計算呼出は最小回数に抑える。
        auto w =
        exp( std::complex<double>(.0,2*M_PI/(double)po2) );
        // そして逆変換の場合は、wの素を複素共役に。
        w = is_inverse ? conj(w): w;
        auto ws = complex<double>(1,0);
        // バタフライダイヤグラム：Wを共有する項をまとめて計算。
        for( int k=0; k<po2m; ++k )
        {
            for( int j=0; j<N; j+=po2 )
            {
                auto pa = &F[j+k];
                auto pb = &F[j+k+po2m];
                auto wfb = ws**pb;
                *pb = *pa - wfb;
                *pa += wfb;
            }// j
            ws *= w;
        }// k
    }// i_level
    return;
}
void lc_inverse_fft( const vector< complex<double> >& a,
                    const vector< int >& ids, const int n_level,
                    vector< complex< double > >* pout )
{
    // inverse_fft
    // 入力信号 a 数値列の、高速フーリエ逆変換を行います。
    // a.size()は２のべき乗数であることが大前提です。
    lc_fft( a, ids, n_level, pout, !0 );
    auto N = a.size();
    for_each( pout->begin(), pout->end(),
             [N](complex<double>& val){val/=N;} );
    return;
}

そしてヘッダーがこうなりまして、

// "fft.h"
#include <iostream>
#include <vector>
#include <complex>

// fft header
int lc_fft_calc_ids( const int N, std::vector< int >* pids );
void lc_fft(
            const std::vector< std::complex<double> >& a,
            const std::vector< int >& ids, const int n_level,
            std::vector< std::complex< double > >* pout, bool is_inverse=0 );
void lc_inverse_fft(
                    const std::vector< std::complex<double> >& a,
                    const std::vector< int >& ids,const int n_level,
                    std::vector< std::complex< double > >* pout );

そしてこれの使い方はずばり以下のようになります。

    // FFT事前計算
    int n_level;
    vector< int > ids;
    {
        n_level = lc_fft_calc_ids( src_img.cols, &ids );
    }    
    // FFT計算
    {
      // .. 繰り返し処理の中などで.. 
      vector< complex<double> > signal;
      {
        // setup "signal" as your FFT input.
      }
      vector< complex<double> > proj, repr;
      lc_fft( signal, ids, n_level, &proj );// FFT変換
      {
        // filter proj somehow as you like
      }
      lc_inverse_fft( proj, ids, n_level, &repr );// FFT逆変換
    }

ここで、参考までに、幅512ピクセルの手書きの繰り返し絵において、各横水平ライン方向の信号を、上記のFFTを使って周波数空間に変換し、繰り返し周期が４の倍数な成分のみを有効としそれ以外の成分をゼロとしてフィルタリングをかけ、再び逆フーリエ変換した結果が、冒頭の図だよ。
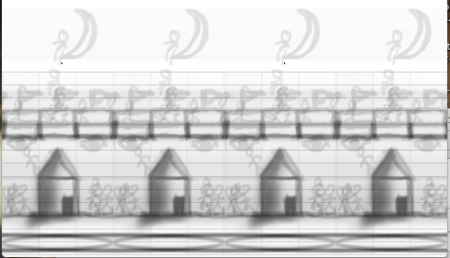
そして更に、深い意味はないのだが、冒頭のもと絵に対し、横軸水平方向に関して高周波成分をカットした例や、繰り返し周期が３の倍数の成分のみからの再構成画像を作成した例も以下に示します。（ちょっと残像みたいのが残っちゃってるのは、いわゆるエイリアシングという、FFTというよりはDFTの本質的な問題で、FFT云々とは別問題な現象。このあたりもまた別に記事を書ければとは思ってます。）

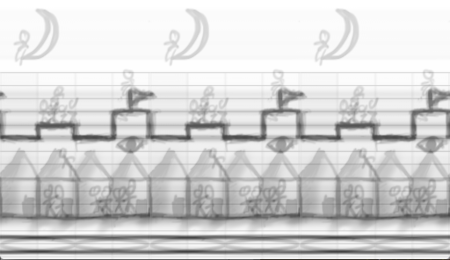
元画像の横幅サイズ512ピクセルですが、これの計算時間はうちのMacMiniで走らせて一瞬で完了します。1秒かかりません。これに対してDFT演算で同じ事をすると、数秒〜10秒くらいは待たされることになります。
長くなりましたが、以上で本記事は終了です。チャオ！
[asin:B008U3LN5U:detail]